Redactle is a game in which you are presented with a Wikipedia page in which most words are redacted, and you need to find the article's title. You can submit as many words as you want, and if the word you submitted is anywhere in the article, it "unredacts" all the occurrences of it, so you can progressively comprehend what the article is about by trial and error.
I usually start by submitting big picture words like "science", "art", "history", "politics", and so on, so that I can get a broad idea of what the article is about depending on how many occurrences are found for each of those words. And then I dig deeper inside what seems to be the broad subject, and so on.
I wondered, what would be the word that would optimally divide the search space of subjects. For example, "science" is probably not a very good word: maybe something like 10% of Wikipedia articles are about science, so if you get a hit on "science" you're lucky, but if you get 0 hit on "science", you didn't gain much information, because you're still in 90% of Wikipedia.
The word that would be optimal would be the one dividing the search space in half. And then, in each of the sub-Wikipedias you are on (the sub-Wikipedia with this one word, and other sub-Wikipedia without this one word), you should find new words that divide each of those spaces in half again, and so on. That would allow a dichotomic search on Wikipedia, and therefore only require log2(Wikipedia size) attempts before you can pinpoint the specific article. That would be very fast even for the size of Wikipedia.
As it happens, Redactle doesn't take its article from all of Wikipedia, but from a specific subset of it: the List of articles every Wikipedia should have. What is referred to as "a Wikipedia" in this page is Wikipedia in one language, so it's about articles that should exist in all languages; but as far as we're concerned, we're using English Wikipedia, for which all of those 10,000 articles exist well and truly.
As I said, the optimal guessing game would allow us to pinpoint articles in log2(Wikipedia size) queries. With only 10,000 articles, this amounts to... 🥁 14. 14 words would be enough to pinpoint any article, assuming the "perfect words" exist at each step. Ok, enough theory, time to put it to practice now.
A mere 55 million words
In order to test this theory, we need 2 things:
- A dataset of those 10,000 Wikipedia articles and all their words.
- An algorithm able to give us the "magic words" that recursively divide the 10,000 articles.
Good news, all of this is easy to get.
Using the Wikimedia and Wikipedia APIs, I downloaded the texts of the 10,000 articles. A mere 55 million words amounting to 445 MB. The biggest article in the dataset is History of Austria with 31,134 words (looks like being at the center of Europe is bound to be eventful), and the smallest one is Phoenicopterus with 60 words (which I have no idea why it's considered an essential article).
For the algorithm to find the "magic words" dividing the articles, we could use the following procedure:
- For each word to test, compute the split produced by this word on the set of articles.
- Choose the word that produces a split closest to 50/50.
- Recursively apply this procedure on:
- The set of articles with this word
- The set of articles without this word
Note that this algorithm is not optimal. For example, if the two best splits are with W1 and W2, it might be better to choose W2 (even if it's the second best) if using W2 first allows W1 to more effectively split the subsets subsequently (the reverse might not hold true). The optimal algorithm would need to find the best combination of words for the tree, which is far more complex. It could be implemented with backtracking, but as it usually results in explosive computational complexity, I assumed the top-down, recursive procedure is the only practical one.
However, instead of implementing this myself, I turned to decision tree learning algorithms to see if they didn't already solve the problem.
Decision trees
The way decision tree learning works is that you give it instances of "classes" having "features", and then it gives you a way to find the class of a brand new instance by following a flowchart (the "decision tree") based on the features.
For example, you could give the algorithm many examples of animals with their characteristics ("features"), and what type of animal they are ("classes"). So you would give:
- A dog has: a spine; milk-producing glands; etc; it is a "mammal"
- A shark has: no spine; no milk-producing glands; etc; it is a "fish"
- Etc
And the algorithm would automatically find the best flowchart (according to some definition of "best") to allow you to classify any animals (depending on its features) you present to it into one of the target "class".
In our case, we would be building an extreme sort of decision tree:
- The "features" are the membership or not of a word in a Wikipedia article. For example, the feature "has the word painting in it" is true for the article "Mona Lisa", but is false for the article "Gravity". So, if we want our classification to be based on a set of 1,000 words, each article is going to have 1,000 boolean features.
- The "classes" are the articles themselves. We don't want the decision tree to help us classify the articles into a smaller set of classes, we actually want it to classify the articles exactly into themselves.
Looking into how such algorithms worked, I saw that they differed from the 50/50 split algorithm I suggested before. They still are top-down (non-backtracking), recursive algorithms, but at each node of the tree, instead of trying to find a perfect 50/50 split, they try to find the feature that creates the most "homogeneous" sub-trees. The "homogeneity" being computed with criteria such as Gini impurity or Shannon entropy.
This has two advantages: the first one is that the algorithm might find a clusters of homogeneous articles that could be pinpointed with less words than the 14 theoretical words. The most extreme example would be if a specific word would belong to 1 single article, which could therefore be found in 1 single guess. The second advantage is that the algorithm may more effectively organize a tree around common lexical fields by identifying "homogeneous" classes of word memberships, unlike the 50/50 splits which may rely on random words out of pure statistical chance.
The drawback, in comparison to the 50/50 split algorithm, is that since the tree is not trying to split nodes in half, the maximum depth of the tree is expected to be more than 14.
10,000 leaves
So I decided to have a try with decision trees. There are obviously various implementations of those, but I settled on the DecisionTreeClassifier from the scikit-learn Python library.
I first built the "index", if you could call it that, of all features for all articles. I decided to use the top 1,000 English nouns as words to test the membership of. The index simply stores the information "word W is in article A" for each of the 1,000 top words and each of the 10,000 articles (10 million memberships tests in total).
I have observed that most articles tend to have only a relatively small subset of the top 1,000 words, so it's lighter to only store, for each article, the words that do belong to it. Furthermore, the top words can be ordered so that only their array index has to be stored for each article.
For extracting words from articles, I split the text around whitespaces, stripped punctuation from both ends, and lowercased the result. We should ideally use the same word-extraction technique that Redactle uses, and from what I have seen on the site, this should be pretty close (notably, Redactle does not match plurals if you submit a singular). Note that there are advanced word extraction libraries such as spaCy, but they considerably slow down the extraction in comparison to trivial techniques.
In the end, this results in a simple JSON index that weights 10 MB and takes 25s to build on my humble computer.
I then ran the aforementioned DecisionTreeClassifier on this index. I didn't know how much time it would take, so I progressively increased the max_depth parameter and each time counted the number of leaves of the tree. Remember, it doesn't necessarily build a balanced tree as it can shortcut to small homogeneous classes, so the number of leaves is expected to be lesser or equal to 2**max_depth.
Note that as long as the tree doesn't classify all articles, articles appearing at the leaf of a tree are not perfectly pinpointed. For example, running the classifier with max_depth=2, we get this tree branch:
|--- shape (True)
| |--- struggle (False)
| | |--- class: 0
| |--- struggle (True)
| | |--- class: 2004_Indian_Ocean_earthquake_and_tsunami
Although the article about 0 indeed contains the word "shape" but not the word "struggle", it is only 1 out of hundreds of articles that have those features. I didn't find a way to easily distinguish between "pure" leaves (perfectly identified) and "impure" leaves (1 instance among others). According to the documentation, the only way to have only pure leaves to set no max_depth at all.
Here are the number of leaves by increasing maximum depths, and the time it took to build on my computer:
| max_depth | Time to build tree (s) | Number of leaves |
|---|---|---|
| 2 | 2.0 | 4 |
| 4 | 2.4 | 16 |
| 8 | 6.8 | 203 |
| 16 | 55.6 | 3533 |
| 32 | 106.2 | 7994 |
| 40 | 107.1 | 8021 |
Trials for depth greater than 40 resulted in the program being killed by my system once it had consumed all my memory. This might be solvable either with more memory or another implementation (maybe), but I'm not sure it would work in the end, considering how few leaves were added between max_depth 32 and 40. So in the end I didn't succeed in classifying the 10,000 articles. Let alone with a tree of reasonable depth (remember that we were initially talking about a depth of 14).
Redacted title to the rescue
I got an idea: Even though Redactle redacts the words of the articles, the size of the words is preserved. This means that we don't have to actually search the solution among all 10,000 articles; we can restrict the search only to articles whose title match the size of the redacted title! This should considerably reduce the search space, and maybe allow us to build complete trees of reasonable depth. Titles with multiple words allow selecting an even stricter subset of the search space.
Here is the distribution of articles according to their title's length:
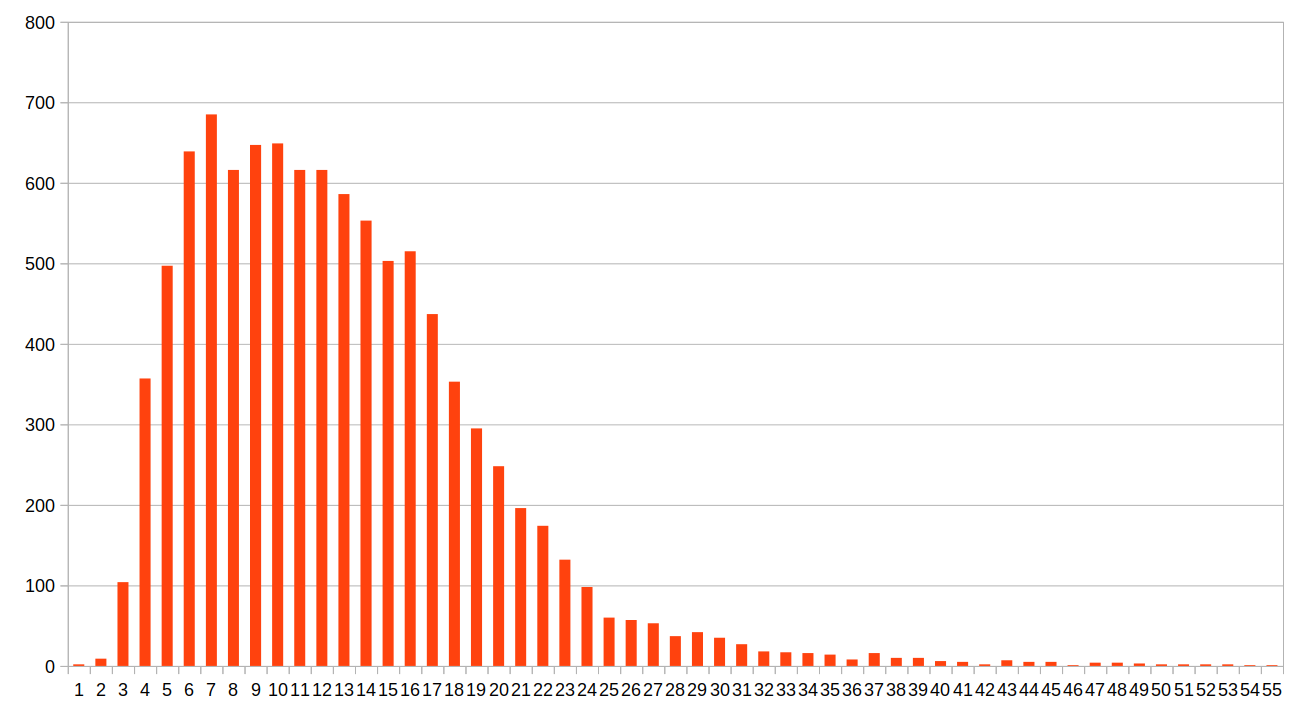
(Although the chart stops at 55, the longest title is International Covenant on Economic, Social and Cultural Rights with 62 characters.)
As we can see, the worst-case is 7-characters titles, for which there are 685 articles. Under our initial log2 criterion, this would require only 10 words to pinpoint each article from this subset. Let's see how a decision tree performs on this subset. This time I ran the classification without any maximum depth and... success 🏆 The resulting tree classifies each and every one of the 685 articles. The deepest leaf is 27 words deep, and the least deep one is only 3 words deep (Sukarno is the only 7-characters title containing the words "command", "representation" and "mirror"). Note that there is an element of randomness in the generation of the tree (which I didn't take the time to investigate), so those specific values are not perfectly reproducible.
On the expected behavior of decision tree to produce homogeneous clusters, I did find some evidence of it. For example, here is a branch at depth 10, following the path (¬north, ¬welfare, ¬error, ¬argument, ¬morning, ¬advantage, drug, ¬series, person), where all the leaves down this branch are related to health.
--- subject (False)
|--- experience (False)
| |--- measure (False)
| | |--- class: Vitamin
| |--- measure (True)
| | |--- class: Vaccine
|--- experience (True)
| |--- class: Measles
--- subject (True)
|--- name (False)
| |--- class: Anxiety
|--- name (True)
| |--- class: Placebo
However, the words chosen for the splits seem very random and brittle. In fact I'm surprised that the word "subject" is not in the Vaccine article, and it feels like the article could be edited for reformulation and completely break the index/tree depending on the words being added or removed. This is the major weakness of this approach.
I guess there would be more things to try to fix this weakness. For example, instead of using the top 1,000 English words for membership testing, maybe more salient words could be extracted from the articles themselves. Moreover, instead of using the membership criterion, maybe the number of occurrences should be used with some threshold (since Redactle prints the number of occurrences for each word). More sophisticated AI methods using embeddings may also be useful.
auto-redactle
In the end, the procedure to solve Redactle with decision trees based on words memberships is the following:
- Accept the redacted title as input.
- Using the index, build a decision tree with unbounded depth on the articles matching the input's words' lengths
- Navigate the decision tree by asking the user whether the word of a node is in the article or not.
- Once at a leaf of the tree, print the solution.
Here is a little demo with a couple of articles. On the left is the Redactle game, and on the right is my terminal navigating the decision tree. The terminal prompts me to test words in Redactle and to input their count of matches (in practice only 0 vs. >0 is used) to advance to the next query.
You can test all of this with my auto-redactle GitHub repository which contains the pre-computed index and the command to run the decision trees on it, as well as commands to build the index from scratch.